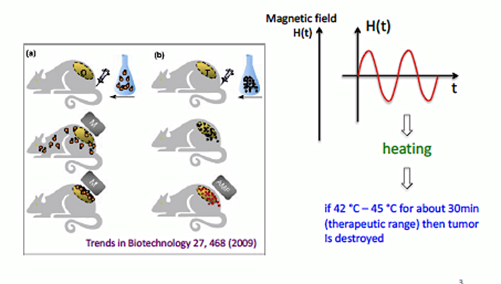
Dr Ondrej Hovorka came in on 21th November to give a seminar on the atomistic modelling of magnetic nanoparticles which are used in biomedical applications, primarily in destroying cancer cells using hyperthermia. In other words, by inducing an increase in body temperature to 42 – 45°C for 30 minutes in the cancerous regions of the body. Unfortunately, it is very difficult to only target tumours with hyperthermia, so instead magnetic nanoparticles are injected into the body, which then accumulate inside cancer cells, and an alternating magnetic field can induce a temperature rise of these nanoparticles.
The key goal of this research is to optimize the heating efficiency by investigating the properties of these nanoparticles, which includes the material of the particles (mainly iron oxides), size and shape of the particles, frequency and range of the magnetic field, interactions with other particles, and the viscosity of the fluid. As such, this requires the use of atomistic modelling of these magnetic materials.
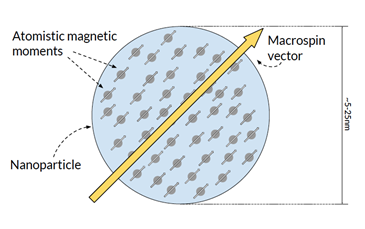
In the atomistic model, a magnetic material can be simulated by a grid of interacting spin vectors, each with unit magnitude. The interactions between spins are described by the spin Hamiltionian and the dynamics of the spin vectors can be simulated using the Landau Lifshitz Gilbert equation. These numerical methods allow us to calculate magnetic properties of the material such as the Curie temperature, which signifies the phase transition between a random paramagnetic phase and the ordered ferromagnetic phase, but it is a computational expensive calculation. It cannot simulate many lattice points, nor can it run for long time scales.
To overcome this issue, we can use a statistical numerical method – the Kinetic Monte Carlo algorithm. This method finds the equilibrium (lowest energy) state of the system, in other words, the configuration at which the rate of transition from state A to state B is exactly the same as the rate from state B to state A. This is also known as the principle of detailed balance and is satisfied by all Monte Carlo methods. Kinetic Monte Carlo, unlike the Metropolis equivalent, uses the actual transition rates between states in the acceptance criteria of a new state. We, therefore, get the natural time scales for phase transitions rather than the iteration count. Thus, important magnetic properties, such as entropy, average magnetisation and internal energy can be plotted as a function of time. Such simulations was run on magnetic nanoparticles, which consisted of three spin moments and their hysteresis cycle was evaluated. The key results from these computation experiments was that ensembles of different arrangements of 100 particles displayed very different hysteretic cycles. This will, in future, be expanded to optimizing the particles cluster for efficient heat transfer required for hyperthermia.
Posted by Vanessa Nehruji
