On 16th May 2019, Chris Skylaris gave an hour-long seminar regarding his work on the cutting edge of scaling quantum computational chemistry simulations to cope with the demand of more complex systems. Here, we present a summary of his presentation.
High performance computing (HPC) has enabled the advancement of computational experimentation in a wide array of fields. Computational Chemistry is no exception; physical calculations are performed for a large number of particles in complex systems, and this is an ideal context for such HPC techniques.
With the advent of quantum theory in the 20th century, the interactions of simple chemical systems could be solved analytically with the concept of wavefunctions and orbital theory. Schrödinger’s equation, an analytical expression that solves for the wavefunctions of the system, can be performed for large systems using numerical approximations. The dynamics of molecular systems, the structure of newly developed materials, and spectral analysis can all be performed with knowledge of the molecular energy, and black box tools now exist to allow chemists to experiment freely with these tools. For large systems, however, these techniques quickly become an immense task even for the most advanced computational schemes.
While the Schrödinger equation allows the wavefunctions to be computed exactly, the computational expense makes it infeasible to be applied to the latest research in Chemistry. In the late 20th century, Density Functional Theory (DFT), an approximation that solves instead for the charge density distribution of the system, was developed. This new iterative scheme allowed for larger systems to be explored with further approximations to the various energy and correlation terms involved. Although the application of DFT continues to be an active field of research, its performance scales cubically with the system size; simulations of roughly 500 atoms can be implemented with the limit of current computing power.
Linear Scaling with ONETEP
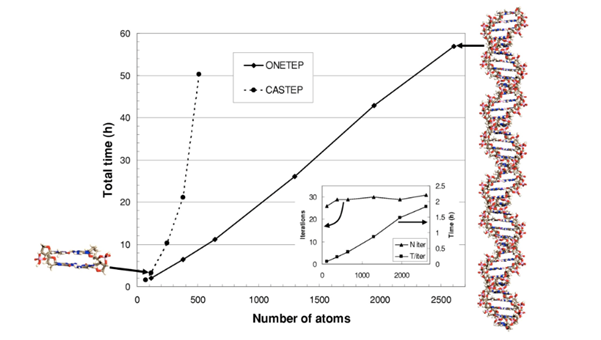
The impact of cubic scaling on execution times has long been the limiting factor for the complexity that can be modelled with DFT. Prof. Skylaris’ ONETEP software (Order-N Electronic Total Energy Package), first published in 2005, manages to recover linear scaling: that is, where the computation time increases linearly with the number of atoms. This represents a significant advantage over traditional, cubic-scaling DFT codes; results can be obtained in less time, or more complex molecules can be simulated.
ONETEP achieves linear scaling by use of assumptions in the traditional DFT method. Most notably, typical molecular orbitals – models that describe the position of electrons around molecules – are replaced with so-called localised orbitals that cover a smaller portion of the molecule, but maintain as much information as possible about the original positions. The size of these localised orbitals can be adjusted in order to determine the size that both retains the maximum amount of information, whilst shrinking the size as much as possible. Often, however, determining the correct trade-off between speed and accuracy is difficult.
These localised orbitals are represented by psinc functions, periodic (i.e.
repeating) sine-waves. The psinc
function has a well-defined – but non-trivial – inverse Fourier Transform,
which allows it to be converted from a function of frequencies into a function
of time. All
quantities in ONETEP are ultimately expressed as psinc functions, which means that ONETEP is essentially a linear
reformulation of the traditional DFT approach.
Applications
This technique has the potential to be far-reaching in its ability to extend the study of recent developments in technology and medicine. Organic Photovoltaics use layers of organic materials as opposed to traditional semiconductors within solar cells to convert sunlight into energy. The region of the organic materials through which the charge is transferred, and the charged particles themselves, must be thoroughly modelled in order to understand the performance of such devices, as well as to make improvements in the future. ONETEP can be used to model the charged states, giving insights into the optimum orientation of molecules for efficient charge transfer.
Posted by Jack Tyler and James Waters
